Understanding Complex Numbers
Definition
A complex number is any grouping of both real and imaginary numbers. Let's look real quick at what an imaginary number is.
Imaginary Numbers
Mathematicians eventually decided to get over the whole √-1 problem, so they defined what we know today as imaginary numbers, usually abbreviated i, though sometimes (such as when solving circuits) you'll see it as j. By defining imaginary numbers, mathematicians were able to get real (non-imaginary) solutions where they previously could not.
Obviously the imaginary number is going to have some properties to it, the biggest and most important of which is that i2 = -1. Other than that, imaginary numbers can be treated as if they were variables.
Complex Numbers
Complex numbers will arise when you add real numbers with imaginary numbers. Usually they are expressed in either cartesian form or polar form.
Cartesian Form
Cartesian form is especially simple. You take your real numbers and your imaginary numbers and put them together with a plus sign between them! So let's say you have an imaginary number of -2 and a real number of 3. The correct answer to the addition of the two would be: 3 - 2i.
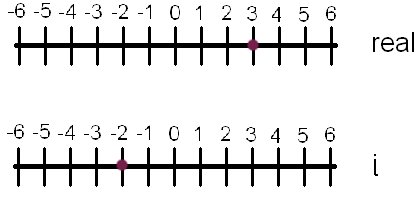
The purple dots represent each of these values. But let's say we add the two values together as in the previous example. How is this depicted graphically?
Well, the answer here cannot be expressed on a single number line. We need to combine the two number lines into a graph, but this is not a normal graph. The y-axis of this graph is reserved for imaginary numbers only. The thing you must understand is that this graph cannot show a real number coordinate point such as (1,2) or (-7, 13). This graph shows complex numbers.
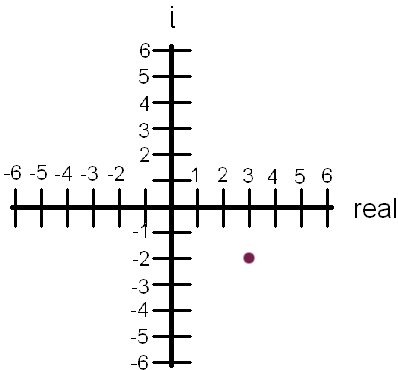
Do you see? The above graph shows you where the complex number 3 - 2i is located.
Polar Form
It is often (believe it or not) helpful to put a complex number in polar form. Polar form tells you the distance (radius) of the complex number (that purple dot) from the origin, as well its angle from the right side of the x-axis. It contains all of the information that the cartesian form does, just in a different format.
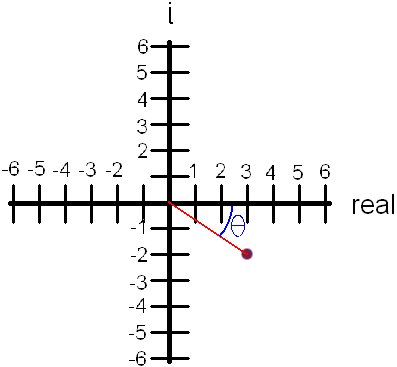
So you probably have two very good questions. One--how do you find the distance, and two--how do you find that angle.
Let's tackle the distance first. The first step is to forget that it's a "special" graph and just treat it from here on out like a normal one. Doing that, we can see the following triangle:
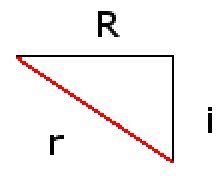
That big red line is the line we drew from the origin to the complex number (I removed the purple dot). The distance, then, is 'r' (radius). The length of the triangle, x, is the value of the real number, and the height, y, is the value of the imaginary number (so -2i would become just -2).
Since this is a right triangle, the Pythagorean theorem will work. So, r2=x2 + y2. Take the positive value (since there is no such thing as a negative distance) of the square root of r2 to get r.
So what about that angle θ? Well, we know from basic trig that the tangent of θ the opposite over adjacent side, so:
tan(θ) = y/x
&theta = arctan (y/x)
Remember that to keep your signs! If x or y is negative, leave that number in there! It wasn't too important with the radius since we squared the number, but here it is important. Just for kicks, see how leaving off a sign changes your answer!
And that's it! You're done! You have both the radius and the angle. Write both of those down, draw a big box around it, and grin like there is no tomorrow, 'cause that's all there is to it.
